Abstract
In the previous chapters, we have briefly introduced applications of copulas to analyses of rainfall, streamflow, drought, water quality, and compound extremes, as well as network design. In this chapter, we will introduce suspended sediment transport. Two case studies will be discussed to (i) apply copulas to construct the discharge-sediment rating curve using the Yellow River dataset; and (ii) investigate the dependence among precipitation, discharge, and sediment yield using the event-based dataset retrieved from the flume #3 at Santa Rita experimental watershed.
16.1 Discharge-Sediment Rating Curve Construction
In this section, application of copulas will be illustrated for modeling suspended sediment transport in regard to discharge-sediment rating curve by:
i. Identifying the study region and collecting discharge and suspended sediment data
ii. Applying the mixed copula that may reasonably capture the upper, lower, and overall dependence to model the discharge-suspended sediment data
iii. Comparing the performance of the copula approach to the classic USGS discharge-suspended sediment rating equations
iv. Interpreting the results according to the underlying surface and channel characteristics
The Yellow River, the most famous sediment-rich river system in the world, is used here as a case study for discharge-sediment rating curves. More specifically, sediment transport is studied for the middle reach of the Yellow River basin. The middle reach is the major sediment source area supplying 90% of the total sediment yield and 38% of the total water resources of the middle Yellow River (MYR) basin. Geologywise, the underlying surface materials change dramatically from north to south, varying from soft rock (i.e., Pisha Rock by locals), sand, loess, to rock mountains (Li and Li, 1994; Wang et al., 2007; Ni et al., 2008) with the median particle size decreasing from north (0.088 mm) to south (0.018 mm). To evaluate the study, we choose four representative stations for each geologically identified unique underlying surface: (1) typical loess – SuiDe, (2) soft-rock sand – Wangdaohengta, (3) rock mountain – Liujiahe, and (4) sand – Gaojiabao. Throughout the case study, we will apply both the classic USGS rating equation and copulas and also compare their performance. To prepare the dataset, the discharge values less than average discharge will be dropped out of the dataset, since we are more concerned with the large amount of suspended sediment transported during runoff events.
The discharge-sediment rating curve has been commonly applied to forecast suspended sediment yield or concentration. The classic USGS sediment rating curve (i.e., Equation (16.1)) through either power function or log-linear function has been commonly applied to achieve this end:
In the previous chapters, we have discussed different types of copulas as well as their applications. In this section, we will apply mixed copula. Let U and V represent the marginals of discharge and suspended sediment, respectively; then we can write the mixed copula as follows:
Commonly, copulas chosen are the copula with λL≠0λL≠0, the meta-Gaussian copula, and the copula with λU≠0λU≠0. Here we will choose the survival Gumbel–Hougaard copula, Gumbel–Hougaard copula, and Gaussian copula as the mixture. The survival Gumbel–Hougaard copula mirrors the Gumbel–Hougaard copula. As a result, the survival Gumbel–Hougaard copula has the lower-tail dependence. With the preceding mixture, Equation (16.2) may be rewritten as follows:
 (16.3)
(16.3)In Equation (16.3), the survival Gumbel–Hougaard copula (CSGH ) can be expressed as follows:
) can be expressed as follows:
 (16.3a)
(16.3a)Again, denoting cc as the copula density, the copula density of CSGH can be given as follows:
can be given as follows:
 (16.3b)
(16.3b)The lower- and upper-tail dependence coefficient is given for the survival Gumbel–Hougaard and Gumbel–Hougaard copula as follows:
 (16.3c)
(16.3c)Substituting Equation (16.3a) into Equation (16.3), the density function for the mixture copula can be given as follows:
Similar to the discussions in other application chapters, to predict the suspended sediment, one needs to estimate the expected suspended discharge with E(SSL| Q = q)ESSLQ=q from
Equation (16.5) may be also called as the median forecast. Applying the copula theory, Equation (16.5) may be rewritten as follows:
In Equation (16.5a), P(FSSL ≤ FSSL(ssl)| FQ = FQ(q))P(FSSL≤FSSLssl|FQ=FQq) can be written through copula as follows:
 (16.5b)
(16.5b)Let hFSSLFQθ=∂CFSSLFQθ∂FQFQ=FQq ; we will have the following:
; we will have the following:
The 90% bound may be written through VaR(5%) (i.e., lower bound) and VaR(95%) (i.e., upper bound) as follows:
 (16.7)
(16.7)With the computed FSSL,FSSL5%,FSSL95% , we usually compute the corresponding value in the real domain with the fitted parametric marginal distributions. In this case, we will use the kernel density function (with a normal kernel) with the positive support to estimate the projected sediment yield. Application of the kernel density function for prediction avoids the possible ill-identification of the marginal distributions due to the very high skewness. From the sample statistics listed in Table 16.1, it is seen that sediment yield is heavily skewed and tailed.
, we usually compute the corresponding value in the real domain with the fitted parametric marginal distributions. In this case, we will use the kernel density function (with a normal kernel) with the positive support to estimate the projected sediment yield. Application of the kernel density function for prediction avoids the possible ill-identification of the marginal distributions due to the very high skewness. From the sample statistics listed in Table 16.1, it is seen that sediment yield is heavily skewed and tailed.
Table 16.1. Sample statistics of sediment yield for four selected stations.
| Station | Mean (kg/s) | Standard deviation (kg/s) | Skewness | Kurtosis |
|---|---|---|---|---|
| Suide | 11.262.25 | 32.037.33 | 7.54 | 86.83 |
| Gaojiabao | 1.273.16 | 7.481.30 | 12.24 | 185.30 |
| Wangdaoheng | 6.260.81 | 29.372.95 | 7.46 | 62.33 |
| LiujiaHe | 11.698.75 | 46.025.54 | 9.28 | 115.36 |
Parameters of the mixture copula are estimated with the pseudo-MLE. The Weibull plotting-position formula is applied to compute the empirical marginals. In the case of model parsimony, the copula will be dropped out of the mixture if its corresponding weight is less than 0.1. For example, if the weights for both the Gaussian (w2)w2) and survival Gumbel–Hougaard copula (w3)w3) are less than 0.1, the mixture copula will be reduced to the Gumbel–Hougaard copula. With this procedure and the maximum likelihood applied to pseudo-observations (i.e., the empirical marginal of discharge and suspended sediment), Table 16.2 lists the estimated parameters of four stations from both copula approach as well as the USGS log-linear regression equations. The results of copula approach in Table 16.2 indicate that the Gumbel–Hougaard copula is the only copula needed based on the model selection procedure (i.e., only consider the copulas with the weight higher than 10% in the mixture). This is quite understandable due to the procedure of data processing: (1) omit the [discharge, sediment] pair when the discharge is lower than the average discharge; and (2) omit the [discharge, sediment] when the sediment yield is less than 0.5% of the average sediment yield.
Table 16.2. Parameters estimated for the discharge-sediment rating curve from the copula.
| Underlying | Geographic characteristics | Copula | USGS | ||||
|---|---|---|---|---|---|---|---|
| Surface | Station | Area (km2) | Slope | Gaussian | GH | SGH | [a∗, b]a∗b |
| Loess | Suide | 3893 | 22.99a | – | 3.071 | – | [1.388, 2.254] |
| Sand | Gaojiabao | 2095 | 0.74 | – | 1.863 | – | [–2.373, 2.822] |
| Soft-rock | Wangdaohengta | 3390 | 0.29 | – | 2.955 | – | [–0.023, 2.134] |
| Rock mountain | Liujiahe | 2361 | 44.25a | – | 2.544 | – | [–0.629, 2.595] |
Note: a The percentage of the slope steeper than 1.5%.
To visually compare the copula approach with the USGS equation, Figure 16.1 compares the fitted copula function and USGS equation (in Figure 16.1A) as well as their forecast power (in Figure 16.1B). The forecast results (Figure 16.1B) are listed in Table 16.3.
Table 16.3. Comparison of forecast power of copula and USGS approaches.
| Q (cms)a | SSY(kg/s)a,b | Copulac | USGSc | Q (cms) | SSY(kg/s) | Copula | USGS |
|---|---|---|---|---|---|---|---|
| Suide station | Liujiahe station | ||||||
| 97.7 | 86,073.7 | 76,957.20 | 122,621.87 | 128 | 110,976 | 89,958.95 | 156,852.25 |
| 127 | 87,249 | 112,057.81 | 221,483.23 | 184 | 114,632 | 131,095.07 | 402,279.65 |
| 104 | 92,040 | 84,049.35 | 141,170.48 | 196 | 13,1908 | 138,174.95 | 473,956.12 |
| 138 | 96,462 | 125,758.45 | 267,092.44 | 147 | 133,182 | 106,072.00 | 224,639.69 |
| 113 | 101,022 | 94,727.58 | 170,214.45 | 210 | 144,060 | 145,989.60 | 566,893.19 |
| 164 | 103,812 | 158,278.90 | 394,136.30 | 192 | 158,976 | 135,863.41 | 449,260.01 |
| 164 | 103,812 | 158,278.90 | 394,136.30 | 326 | 167,890 | 269,808.11 | 1774,991.57 |
| 164 | 104,960 | 158,278.90 | 394,136.30 | 254 | 182,626 | 176,613.58 | 928,772.23 |
| 115 | 109,020 | 971,64.83 | 177,081.01 | 297 | 184,140 | 229,288.33 | 1,393,760.25 |
| 169 | 111,033 | 164,714.59 | 421,742.65 | 241 | 185,811 | 165,330.82 | 810,388.83 |
| 138 | 112,056 | 125,758.45 | 267,092.44 | 275 | 209,000 | 200,007.38 | 1,141,415.85 |
| 176 | 121,968 | 173,833.17 | 462,146.64 | 282 | 210,090 | 208,958.40 | 1,218,358.53 |
| 158 | 124,346 | 150,666.33 | 362,375.14 | 279 | 210,924 | 205,069.38 | 1,185,005.20 |
| 158 | 124,346 | 150,666.33 | 362,375.14 | 264 | 215,952 | 187,018.04 | 1,026,674.31 |
| 178 | 139,018 | 176,451.53 | 474,069.33 | 252 | 221,004 | 174,722.80 | 909,911.49 |
| 198 | 146,916 | 202,558.00 | 602,680.75 | 322 | 224,112 | 264,266.82 | 1,719,020.60 |
| 204 | 147,900 | 210,140.26 | 644,633.46 | 407 | 231,990 | 385,953.85 | 3,157,341.74 |
| 204 | 157,896 | 210,140.26 | 644,633.46 | 272 | 236,096 | 196,331.14 | 1,109,380.45 |
| 231 | 200,046 | 241,611.05 | 853,096.43 | 343 | 242,158 | 293,295.70 | 2,025,308.37 |
| 251 | 213,099 | 262,330.06 | 1,028,698.61 | 438 | 244,842 | 433,235.20 | 3,819,957.26 |
| 309 | 224,952 | 328,976.59 | 1,643,641.81 | 375 | 304,125 | 338,053.86 | 2,552,848.84 |
| Gaojiabao Station | Wangdaohengta Station | ||||||
| 23.9 | 13,503.5 | 6,01.10 | 723.16 | 51.1 | 3,980.69 | 3,729.80 | 4,313.90 |
| 36.1 | 14,692.7 | 2,573.53 | 2315.61 | 36.5 | 4,526 | 2,102.76 | 2,104.27 |
| 42.3 | 15,397.2 | 3,527.72 | 3621.66 | 43.1 | 4,870.3 | 2,825.67 | 2,999.91 |
| 53.5 | 15,408 | 4,535.20 | 7027.18 | 30.5 | 5,215.5 | 1,503.63 | 1,434.50 |
| 38.3 | 16,200.9 | 2,973.66 | 2736.31 | 66 | 6,217.2 | 5,577.68 | 7,446.53 |
| 57.9 | 18,296.4 | 5,916.65 | 8783.01 | 31.9 | 7,081.8 | 1,636.34 | 1,578.65 |
| 60.3 | 18,873.9 | 7,124.40 | 9849.59 | 120 | 7,992 | 22,696.57 | 2,6662.30 |
| 51.5 | 19,415.5 | 4,171.17 | 6310.86 | 84.8 | 11,108.8 | 9,176.62 | 12,711.38 |
| 51.6 | 20,691.6 | 4,185.74 | 6345.50 | 50.4 | 11,491.2 | 3,650.05 | 4,188.80 |
| 54.1 | 22,289.2 | 4,674.29 | 7251.86 | 51 | 11,985 | 3,718.39 | 4,295.91 |
| 70.3 | 22,917.8 | 11,992.07 | 15186.77 | 138 | 12,806.4 | 32,135.92 | 35,925.11 |
| 72.9 | 23,182.2 | 14,130.16 | 16825.71 | 97.4 | 19,967 | 13,019.05 | 17,082.53 |
| 88.4 | 24,663.6 | 21,679.14 | 28989.32 | 74.4 | 25,072.8 | 6,926.16 | 9,615.22 |
| 57.9 | 25,012.8 | 5,916.65 | 8783.01 | 87.6 | 25,579.2 | 9,919.53 | 13,623.63 |
| 52.9 | 26,502.9 | 4,409.92 | 6807.06 | 182 | 27,482 | 59,230.34 | 64,838.33 |
| 59.4 | 29,581.2 | 6,633.95 | 9440.36 | 146 | 28,032 | 36,673.52 | 40,514.79 |
| 73 | 34,310 | 14,219.50 | 16890.92 | 121 | 29,403 | 23,187.85 | 27,138.58 |
| 70.8 | 40,780.8 | 12,360.18 | 15493.56 | 134 | 36,448 | 29,939.41 | 33,739.90 |
| 89.7 | 423,38.4 | 22,507.14 | 30208.52 | 174 | 45,240 | 53,886.25 | 58,908.88 |
| 98.5 | 46,886 | 30,084.53 | 39338.98 | 89.6 | 57,881.6 | 10,489.26 | 14,295.85 |
| 108 | 50,220 | 37,758.66 | 51011.10 | 122 | 63,440 | 23,683.93 | 27,619.34 |
Notes: a Observed; b: SSY stands for suspended sediment yield; c forecast from discharge (Q) in column 1.
From Figure 16.1 and Table 16.3, we can reach the following conclusions.
Figure 16.1 Plots of discharge and suspended sediment yield for all four stations: (A) fitted copula function and USGS equation; (B) comparison of the forecast power between the copula function and USGS equation).
16.1.1 Stations Suide and Liujiahe
These two stations yield similar results as follows:
a. The relation between discharge and suspended sediment yield is obviously nonlinear for the discharge lower than 100 cms and the relation tends to be linear in logarithm domain for the discharge higher than 100 cms. The fitted copula function properly follows this observed trend.
b. The linear USGS regression equation in the logarithm domain (or the power function in real domain) tends to overestimate the suspended sediment yield for discharge higher than 100 cms at both locations.
c. From the forecast results, it again shows that the copula-based approach provides a very reasonable forecast for sediment yield, especially in the case of high sediment yield due to high runoff events. During the flood season, one may directly use the copula approach to project the possible suspended sediment rushing downhill.
d. For the same dataset for testing the forecast power, the USGS equation significantly overestimates sediment yield. The results obtained directly from the USGS equation are not reliable.
16.1.2 Stations Gaojiabao and Wangdaohengta
Like the stations at Suide and Liujiahe, similar results are obtained for Gaojiabao and Wangdaohengta stations as discussed in what follows:
a. Unlike the Suide and Liujiahe stations, the scatterplots tend to be more linear at Gaojiabao and Wangdaohengta stations. As a result, both the copula and USGS equation approaches follow the trend reasonably well.
b. The forecast performance using both approaches reach very similar results. The suspended sediment at Wangdaohengta is better forecasted than that at Gaojiabao (which exhibits as more of a nonlinear relation than that at Wangdaohengta).
Besides the obtaining the preceding results by grouping the stations with similar results together, we may gain more information from geomorphological and geological aspects:
i. The slope of the river channel in different subreaches may be the main deciding factor for the relation between discharge and suspended sediment. The higher the percentage of slope (i.e., steeper than 1.5%), the more nonlinear the relation becomes. As the flattest station, Wangdaohengta reaches the most linear relation compared to all other stations (Figure 16.1; Wangdaohengta (A)). With the increase of slope, the nonlinearity becomes more and more obvious from low to high as Gaojiabao, Suide, and Liujiahe.
ii. For the sections with steep river channels, the sediment from the upper subreach may be easier to be transported as suspended sediment. The local sediment may also be easier to be picked up and transported as suspended sediment. Suide station, located in the typical Loess region, may be a good example to carry both sediment from the upper subreach and local sediment as suspended sediment during flood events. Liujiahe station, located in the rock mountain region, may be a good example to carry sediment from upper subreach as suspended sediment.
iii. For the sections with flat river channels, for the same amount of runoff, the flow velocity and the corresponding shear stress will be significantly reduced. As a result, the suspended sediment from the upper subreach may be deposited as a bed load rather than suspended sediment. Wangdaohengta station in the soft-rock region may be a good example to illustrate sediment deposition in a flat river channel and linear relation in the logarithm domain. Gaojiabao station in the sand region, which is slightly more nonlinear than Wangdaohengta station, may be a good example to explain the deposition with more suspended sediment transported than Wangdaohengta: (a) the overall slope at Gaojiabao is slightly steeper than that at Wangdaohengta and (b) the particle size of the underlying sand surface is generally smaller than that of soft-rock.
Above all, this case study suggests to apply the copula approach to construct the discharge-sediment rating curve for steeper channels, while the USGS regression equation in the logarithm domain may be safely applied for flatter channels.
Applying the sediment-rich middle reach of Yellow River with four major underlying surfaces, the case study indicates the following:
The USGS regression equation may work as well as the copula-based method when the channel is flat. In this case, sediment may be harder to be transported or it may actually move as bed load rather than suspended sediment due to low flow velocity and low shear force. For the flat channel, the type of underlying surface does not seem to be the dominating factor for the suspended sediment transport.
The copula-based method works much better than the USGS regression equation when the channel is steep. For the steep channel, the relation of discharge and suspended sediment in the logarithm domain is no longer linear. The nonlinearity for the discharge-suspended sediment rating curve is dependent on the underlying surface when the discharge is lower than a certain threshold. However, for the discharge higher than the certain threshold, the nonlinear relation seems to be replaced by the linear relation similar to the linear relation for the flatter channel.
16.2 Dependence Study of Precipitation, Discharge, and Sediment Yield
16.2.1 Event-Based Sediment Dataset
Precipitation, discharge, and sediment yield are related. In this section, we are going to use the events collected from Flume #3 at Santa Rita experimental watershed (1975–2018) as the case study to further evaluate this interrelation. In the available dataset, sediment data were missing from 1990–2000. Figure 16.2 shows the watershed map retrieved from tucson.ars.ag.gov (USDA, n.d.). As shown in Figure 16.2, Flume 3 covers a small area of 6.81 acres. Table 16.4 lists the events selected from the available dataset.
Table 16.4. Selected rainfall, discharge, and sediment data (flume 3, Santa Rita watershed).
| Dates | Sediment yield (lb) | Rainfall depth (inch) | Runoff volume (ft3) | Peak runoff (cfs) |
|---|---|---|---|---|
| 9/1/75 | 5,512 | 1.33 | 4,759 | 7.506 |
| 8/22/76 | 1,329 | 0.35 | 2,002 | 4.909 |
| 9/5/77 | 1,426 | 0.41 | 3,116 | 4.526 |
| 9/11/77 | 2,279 | 0.45 | 4,027 | 4.157 |
| 10/6/77 | 9,974 | 2.32 | 16,180 | 14.7 |
| 12/28/77 | 5,833 | 0.36 | 4,948 | 4.464 |
| 8/10/83 | 54,092 | 1.32 | 17,350 | 12.91 |
| 10/19/83 | 14,826 | 0.93 | 11,800 | 8.337 |
| 10/3/84 | 1,990 | 0.51 | 3,604 | 4.328 |
| 7/10/88 | 12,696 | 1.22 | 9,240 | 8.171 |
| 8/7/89 | 4,481 | 2.1 | 17,060 | 6.309 |
| 8/11/89 | 20,256 | 1.43 | 14,260 | 10.06 |
| 6/22/00 | 2,015 | 0.69 | 4,073 | 5.798 |
| 8/17/00 | 1,924 | 0.68 | 5,733 | 5.26 |
| 7/22/02 | 4,698 | 1.15 | 8,385 | 7.565 |
| 8/28/02 | 5,515 | 0.455 | 5,453 | 6.96 |
| 9/6/02 | 14,820 | 2.765 | 20,360 | 21.51 |
| 7/22/03 | 17,146 | 0.86 | 10,820 | 14.84 |
| 4/1/04 | 4,869 | 0.565 | 4,483 | 5.981 |
| 7/13/04 | 14,654 | 1.185 | 11,420 | 13.22 |
| 7/23/04 | 69,546 | 2.2 | 35,770 | 23.22 |
| 8/5/04 | 10,980 | 0.605 | 6,282 | 7.565 |
| 7/31/05 | 4,256 | 0.5 | 4,426 | 5.616 |
| 8/2/05 | 13,187 | 0.64 | 6,508 | 11.67 |
| 8/14/05 | 14,623 | 0.84 | 5,868 | 5.26 |
| 8/23/05 | 14,358 | 1.31 | 9,362 | 4.395 |
| 9/8/05 | 4,748 | 0.355 | 2,730 | 4.912 |
| 7/4/06 | 11,577 | 1.04 | 7,295 | 10.69 |
| 7/29/06 | 11,087 | 0.93 | 7,734 | 7.979 |
| 9/8/06 | 5,134 | 0.305 | 3,175 | 5.437 |
| 9/12/06 | 10,304 | 0.305 | 3,416 | 4.737 |
| 7/12/07 | 12,520 | 0.87 | 5,979 | 6.96 |
| 7/31/07 | 12,011 | 0.765 | 5,056 | 5.616 |
| 8/1/07 | 26,797 | 1.19 | 17,140 | 14.29 |
| 9/16/07 | 9,385 | 0.635 | 5,486 | 6.96 |
| 7/19/08 | 54,921 | 3.425 | 41,500 | 29.04 |
| 7/22/08 | 34,092 | 1.17 | 13,740 | 11.18 |
| 8/1/08 | 36,473 | 1.335 | 21,320 | 16.55 |
| 8/31/08 | 23,429 | 1.365 | 16,120 | 13.22 |
| 9/10/08 | 26,849 | 1.45 | 16,320 | 13.75 |
| 9/11/08 | 13,059 | 1.02 | 8,666 | 5.616 |
| 7/3/09 | 5,730 | 2.135 | 23,870 | 15.97 |
| 7/3/09 | 38,128 | 2.135 | 23,870 | 15.97 |
| 7/8/09 | 29,706 | 1.505 | 16,130 | 10.45 |
| 9/7/10 | 8,498 | 0.61 | 5,520 | 5.26 |
| 7/20/11 | 21,671 | 1.06 | 11,750 | 9.977 |
| 8/18/11 | 14,785 | 0.84 | 7,442 | 10.69 |
| 9/9/11 | 11,197 | 1.42 | 6,409 | 7.771 |
| 9/9/11 | 4,460 | 1.42 | 6,409 | 7.771 |
| 9/13/11 | 19,549 | 0.88 | 13,820 | 15.12 |
| 9/13/11 | 22,942 | 0.88 | 13,820 | 15.12 |
| 7/14/12 | 12,690 | 0.69 | 6,930 | 8.407 |
| 9/4/12 | 6,072 | 0.4 | 3,527 | 3.902 |
| 3/1/14 | 14,610 | 1.49 | 9,354 | 4.912 |
| 7/9/14 | 27,849 | 1.325 | 14,660 | 15.69 |
| 7/11/14 | 10,553 | 0.525 | 4,029 | 4.395 |
| 7/13/14 | 39,104 | 1.66 | 19,180 | 18.03 |
| 9/6/14 | 14,009 | 0.55 | 5,492 | 10.45 |
| 10/8/14 | 7,612 | 0.415 | 3,315 | 4.737 |
| 6/30/15 | 3,737 | 0.36 | 2,053 | 4.229 |
| 6/30/15 | 2,538 | 0.36 | 2,053 | 4.229 |
| 9/3/15 | 10,678 | 0.97 | 4,356 | 4.065 |
| 12/12/15 | 14,549 | 1.095 | 7,623 | 7.565 |
| 6/10/16 | 10,971 | 0.53 | 4,786 | 9.067 |
| 6/30/16 | 10,124 | 0.44 | 5,451 | 9.291 |
| 7/1/16 | 9,442 | 0.61 | 7,146 | 8.407 |
| 7/26/16 | 12,959 | 0.685 | 3,850 | 5.616 |
| 7/27/16 | 13,071 | 0.645 | 5,682 | 11.42 |
| 7/30/16 | 10,930 | 0.755 | 6,323 | 7.565 |
16.2.2 Empirical Analysis of Sediment Dataset
Before we proceed with the copula application, we first perform an empirical analysis using the sediment dataset. The sample statistics listed in Table 16.5 show that the target variables are skewed to the right and tailed. As shown in Figure 16.3, the histogram and kernel density frequency yield the same results. It should be noted that the support of the kernel density needs to be positive based on the nature of dataset. Table 16.6 lists the rank-based Kendall and Spearman correlation coefficients of the pair variables. Results indicate the positive dependence for all pair variables. The scatter plots and chi- and K-plots further confirm the positive dependence structure for the pair variables, as shown in Figures 16.4 and 16.5.
Table 16.5. Sample statistics for rainfall, runoff, and sediment events.
| Variables | Mean | Standard deviation | Skewness | Kurtosis |
|---|---|---|---|---|
| Sediment yield (lb) | 14,896.16 | 13,192.28 | 2.01 | 7.54 |
| Rainfall depth (inch) | 1.01 | 0.62 | 1.48 | 5.61 |
| Runoff volume (ft3) | 9,678.49 | 7,562.99 | 1.94 | 7.58 |
| Peak runoff (cfs) | 9.31 | 5.11 | 1.43 | 5.31 |
Figure 16.3 Histogram and kernel density frequencies for the univariate variables.
| Sediment yield | Rainfall depth | Runoff volume | Peak runoff | |
|---|---|---|---|---|
| Sediment yield | 1 | 0.48 | 0.627 | 0.544 |
| Rainfall depth | 0.626 | 1 | 0.724 | 0.494 |
| Runoff volume | 0.767 | 0.881 | 1 | 0.655 |
| Peak runoff | 0.726 | 0.667 | 0.828 | 1 |
Note: Values in italic denotes the Spearman correlation coefficients.
Figure 16.4 Scatter plots of sediment yields versus rainfall depth, runoff volume, and peak runoff.
Now, with the dependence structure identified, we may further study the dependence with the use of copula theory.
16.2.3 Dependence Study of Runoff Volume and Sediment Yield with Copula Theory
We have shown that the pair variables are positively dependent. Additionally, there exists a higher degree of association between sediment yield versus runoff volume and sediment yield versus peak runoff than that between sediment yield versus rainfall depth. To illustrate the copula application in sediment analysis, we will first do bivariate analysis using sediment yield and runoff volume followed by the multivariate sediment analysis.
Before we apply the copula theory to the sediment yield and runoff volume, we will first compute the tail dependence coefficient. Applying all three empirical tail dependence coefficients LOG, SEC, and CFG, we compute the following: λ̂USEC=0.696,λ̂ULOG=0.683,λ̂UCFG=0.686 . From the computed empirical upper-tail dependence coefficient, there is minimal difference in the results with the use of three approaches. Thus, we may apply the copula belonging to the extreme value family to do bivariate analysis. As discussed in Chapter 4, we will apply the Gumbel–Hougaard copula.
. From the computed empirical upper-tail dependence coefficient, there is minimal difference in the results with the use of three approaches. Thus, we may apply the copula belonging to the extreme value family to do bivariate analysis. As discussed in Chapter 4, we will apply the Gumbel–Hougaard copula.
The empirical probabilities computed from the kernel density with positive support (Table 16.7) are applied to estimate the Gumbel–Hougaard copula parameter. Additionally, Figure 16.6 plots the comparison of kernel density–based CDF with that computed using the Weibull plotting-position formula. The scatter plots of CDFs (i.e., Figure 16.6(c)) visually indicates the upper-tail dependence between sediment yield and runoff volume. Applying the pseudo-MLE, the parameter is estimated as θ = 2.822θ=2.822. The corresponding theoretical upper-tail dependence coefficient is computed as λUGH=2−21θ=2−212.822=0.722 , which is slightly higher than its empirical estimation. Applying the Rosenblatt goodness-of-fit test discussed in Chapters 3 and 4, we compute P=0.31,SnB=0.15
, which is slightly higher than its empirical estimation. Applying the Rosenblatt goodness-of-fit test discussed in Chapters 3 and 4, we compute P=0.31,SnB=0.15 . The results of the goodness-of-fit test further confirm that the Gumbel–Hougaard copula may be properly applied to do bivariate sediment analysis.
. The results of the goodness-of-fit test further confirm that the Gumbel–Hougaard copula may be properly applied to do bivariate sediment analysis.
Table 16.7. Empirical probability computed using kernel density.
| Pair no. | Sediment yield | Runoff volume | Pair no. | Sediment yield | Runoff volume |
|---|---|---|---|---|---|
| 1 | 0.230 | 0.288 | 36 | 0.964 | 0.986 |
| 2 | 0.022 | 0.030 | 37 | 0.898 | 0.766 |
| 3 | 0.027 | 0.114 | 38 | 0.910 | 0.903 |
| 4 | 0.072 | 0.208 | 39 | 0.810 | 0.822 |
| 5 | 0.440 | 0.823 | 40 | 0.847 | 0.826 |
| 6 | 0.245 | 0.308 | 41 | 0.572 | 0.591 |
| 7 | 0.962 | 0.845 | 42 | 0.240 | 0.927 |
| 8 | 0.634 | 0.712 | 43 | 0.917 | 0.927 |
| 9 | 0.057 | 0.163 | 44 | 0.870 | 0.822 |
| 10 | 0.558 | 0.618 | 45 | 0.371 | 0.366 |
| 11 | 0.179 | 0.840 | 46 | 0.787 | 0.710 |
| 12 | 0.764 | 0.780 | 47 | 0.633 | 0.522 |
| 13 | 0.059 | 0.213 | 48 | 0.495 | 0.446 |
| 14 | 0.054 | 0.386 | 49 | 0.178 | 0.446 |
| 15 | 0.190 | 0.577 | 50 | 0.751 | 0.769 |
| 16 | 0.230 | 0.360 | 51 | 0.804 | 0.769 |
| 17 | 0.634 | 0.892 | 52 | 0.557 | 0.486 |
| 18 | 0.699 | 0.680 | 53 | 0.257 | 0.155 |
| 19 | 0.198 | 0.258 | 54 | 0.627 | 0.623 |
| 20 | 0.628 | 0.700 | 55 | 0.856 | 0.789 |
| 21 | 0.982 | 0.977 | 56 | 0.466 | 0.209 |
| 22 | 0.485 | 0.435 | 57 | 0.921 | 0.875 |
| 23 | 0.168 | 0.252 | 58 | 0.606 | 0.363 |
| 24 | 0.577 | 0.454 | 59 | 0.329 | 0.134 |
| 25 | 0.627 | 0.399 | 60 | 0.142 | 0.033 |
| 26 | 0.618 | 0.623 | 61 | 0.085 | 0.033 |
| 27 | 0.192 | 0.080 | 62 | 0.472 | 0.244 |
| 28 | 0.511 | 0.512 | 63 | 0.625 | 0.533 |
| 29 | 0.490 | 0.540 | 64 | 0.485 | 0.291 |
| 30 | 0.212 | 0.120 | 65 | 0.447 | 0.359 |
| 31 | 0.455 | 0.144 | 66 | 0.415 | 0.502 |
| 32 | 0.551 | 0.409 | 67 | 0.568 | 0.189 |
| 33 | 0.530 | 0.319 | 68 | 0.572 | 0.382 |
| 34 | 0.846 | 0.842 | 69 | 0.483 | 0.439 |
| 35 | 0.412 | 0.363 |
Figure 16.6 Comparison of kernel density with the Weibull plotting-position formula and scatter plots of empirical CDFs.
The plots in Figure 16.7 yield the same results in regard to the comparison of (i) empirical Kendall distribution versus parametric Kendall distribution for the fitted Gumbel–Hougaard copula, (ii) the empirical copula versus the fitted Gumbel–Hougaard copula, (iii) the empirical CDF (kernel density approach) versus simulated variates from the fitted Gumbel–Hougaard copula (frequency domain), and (iv) observations versus simulated variates (real domain).
To this end, we have shown that a copula can successfully model the dependence of runoff volume and sediment yield. To better understand the interrelation among rainfall, runoff, and sediment yield, we will study multivariate dependence using rainfall depth, runoff volume, and sediment yield in the following section.
16.2.4 Multivariate Dependence Study of Rainfall Depth, Runoff Volume, and Sediment Yield
To study the multivariate dependence among rainfall depth, runoff volume, and sediment yield, we will apply two approaches: (i) meta-Student t copula and (ii) the vine copula with runoff volume as the center variable. To investigate the ability of using rainfall depth and runoff volume to predict sediment yield, we use the first 59 observations (Table 16.7) to build the dependence model and the last 10 observations to study the predictability of rainfall depth and runoff volume.
Dependence Model with the Meta-Student t Copula
Applying the meta-Student t copula discussed in Section 7.2.2, Table 16.8 lists the estimated parameter (i.e., the correlation matrix and degree of freedom) with pseudo-MLE in which the empirical CDF is again computed with the kernel density function approach. The application of kernel density function allows us to find the empirical CDF of “future” values continuously across ℝ+ℝ+ (listed in Table 16.8 for rainfall depth and runoff volume).
Table 16.8. Estimated parameter for the meta-Student t copula with pseudo-MLE.
| Sediment yield | Correlation matrix Rainfall depth | Runoff volume | Degree of freedom | |
|---|---|---|---|---|
| Sediment yield | 1 | 0.709 | 0.857 | |
| Rainfall depth | 0.709 | 1 | 0.915 | ν = 5.817ν=5.817 |
| Runoff volume | 0.857 | 0.915 | 1 |
We have shown in other chapters that the meta-elliptical copula (i.e., meta-Student t copula here) may be successfully applied to model the dependence structure, since the meta-elliptical copula is built on the transformed data (i.e., univariate meta-Student t transformation) as discussed in Chapter 7. Here, we will proceed to the forecast study for the sediment yield directly using the parameters listed in Table 16.8 and variates in Table 16.9.
Table 16.9. Univariate CDF computed for the last 10 observations using the kernel density function built with the first 59 observations.
| Rainfall depth | Runoff volume | ||
|---|---|---|---|
| Inch | CDF | ft3 | CDF |
| 0.36 | 0.086 | 2,053 | 0.032 |
| 0.36 | 0.086 | 2,053 | 0.032 |
| 0.97 | 0.525 | 4,356 | 0.226 |
| 1.095 | 0.595 | 7,623 | 0.477 |
| 0.53 | 0.225 | 4,786 | 0.266 |
| 0.44 | 0.152 | 5,451 | 0.324 |
| 0.61 | 0.287 | 7,146 | 0.448 |
| 0.685 | 0.342 | 3,850 | 0.179 |
| 0.645 | 0.313 | 5,682 | 0.343 |
| 0.755 | 0.390 | 6,323 | 0.392 |
With rainfall depth and runoff volume known, the conditional distribution of sediment yield for the given rainfall depth and runoff volume may be written using Equation (7.56) as follows:

Applying the median forecast (i.e., P(sediment yield<=S|Rainfall depth = d, Runoff volume = v) = 0.5), we have TS−μs∣d,vΣs∣d,v0.5νS∣d,v=0.5 , where S is the sediment yield forecasted. Using the same approach as that in Example 7.11, the forecasted sediment yields are plotted in Figure 16.8. Figure 16.8 also plots the forecasted sediment yields from bivariate sediment analysis. It is seen that the meta-Student t copula and GH copula (using the same parameter estimated for the entire dataset in Section 16.2.3) yield similar forecast results. Even though the observations fall into the 95% confidence interval constructed using the Student t copula, there exist visible differences among the observations and forecasts.
, where S is the sediment yield forecasted. Using the same approach as that in Example 7.11, the forecasted sediment yields are plotted in Figure 16.8. Figure 16.8 also plots the forecasted sediment yields from bivariate sediment analysis. It is seen that the meta-Student t copula and GH copula (using the same parameter estimated for the entire dataset in Section 16.2.3) yield similar forecast results. Even though the observations fall into the 95% confidence interval constructed using the Student t copula, there exist visible differences among the observations and forecasts.
Figure 16.8 The forecasted sediment yields from trivariate and bivariate sediment analysis.
Dependence Model with Vine Copula
As in the preceding section, the first 59 observations are used to build the vine copula (shown in Figure 16.9), and the last 10 observations are applied for forecast purposes. The Gumbel–Hougaard copula is applied to model the runoff volume and sediment yield as well as rainfall depth and runoff volume of T1, and the Frank copula is applied for T2. The parameters estimated are also shown in Figure 16.9. It is noted that S, V, and D represent sediment yield, runoff volume, and rainfall depth, respectively. Comparisons shown in Figures 16.10 and 16.11 indicate the appropriateness of applying the fitted vine copula to do the trivariate sediment analysis. The Rosenblatt goodness-of-fit test also confirms that the fitted vine copula may properly model the dependence (SnB=0.059,P=0.635) .
.
Figure 16.9 Vine structure and the parameter estimated.
Figure 16.10 Comparison of observations to the simulated variates in frequency domain.
Figure 16.11 Comparison of observations and simulated variates in real domain.
With the fitted vine copula, the median forecast of the sediment yield may be computed using the similar procedure for the second-order copula-based Markov process. In detail, the forecast of sediment yield is performed with the following steps:
1. Compute the empirical CDF for the last 10 observations of rainfall depth (D) and runoff volumes (V), using the kernel density function fitted to the first 59 observed rainfall depth (listed in Table 16.9). Here we apply the assumption that variables are random and the first 59 observations may represent the population statistics.
2. Compute conditional probability p1=PD≤dV=v=∂CGHFdFv3.589∂Fv
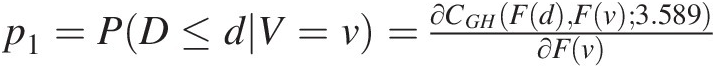 .
.
3. Compute the conditional probability p2 = P(S ≤ s| V = v)p2=PS≤sV=v from P(S ≤ s| D = d, V = v) = 0.5PS≤sD=dV=v=0.5 as: p2=PS≤sV=v=P−1p10.5=CFrank−condtional−1p10.5−2.702
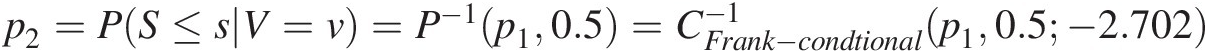 . The conditional Frank copula is listed in Chapter 4.
. The conditional Frank copula is listed in Chapter 4.
4. Compute the probability of the forecasted sediment yield by setting p2 = P(S ≤ s| V = v)p2=PS≤sV=v and Fs=CGH−conditional−1Fvp22.955
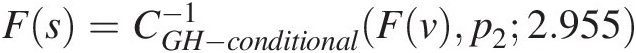 .
.
5. Interpolate the forecasted sediment yield in the real domain with the use of the kernel density fitted to the first 59 observations.
Comparisons in Figure 16.12 indicate a very similar performance between the meta-Student t and vine copula.
Figure 16.12 Comparison of the forecasted sediment yield from vine, Student t, and Gumbel–Hougaard copulas with the observed sediment yield.
16.3 Summary
In this chapter, we apply copulas to (1) suspended sediment analysis by constructing the copula-based discharge-sediment rating curve and (2) bivariate and trivariate sediment analysis with the use of meta-Student t and vine copulas.
Applying the sediment-rich middle reach of Yellow River with four major underlying surfaces, the case study of the discharge-sediment rating curve indicates the following:
The USGS regression equation may work as well as the copula-based method when the channel is flat. In this case, the sediment may be harder to transport or it may actually move as bed load rather than suspended sediment due to low flow velocity and low shear force. For the flat channel, the type of underlying surface does not seem to be the dominating factor for the suspended sediment transport.
The copula-based method works much better than the USGS regression equation when the channel is steep. For the steep channel, the relation of discharge and suspended sediment in the logarithm domain is no longer linear. The nonlinearity for the discharge-suspended sediment rating curve is dependent on the underlying surface when the discharge is lower than a certain threshold. However, for the discharge higher than the certain threshold, the nonlinear relation seems to be replaced by the linear relation similar to the linear relation for the flatter channel.
Using the Flume #3 at Santa Rita experimental watershed as a case study example, the GH copula is applied to model the dependence of sediment yield and runoff volume. It is shown that the GH copula may properly capture both the upper-tail and overall dependence of the sediment yield and runoff volume. According to the nature of the sediment yield, runoff volume, and rainfall depth, the meta-Student t and GH–GH–Frank vine copula are applied to model the trivariate dependence. As shown in the case study, the runoff volume is considered the center variable, and the GH copula may also properly model the bivariate dependence of runoff volume and rainfall depth. The goodness-of-fit studies prove that the meta-Student t and GH–GH–Frank copulas may properly model the dependence. It is also confirmed visually from the simulation study.
Applying the median forecast of sediment yield with known runoff volume and rainfall depth, the forecast study shows the meta-Student t and vine copulas yield very similar forecast results. The forecast study shows there exist significant differences between forecasted and observed sediment yields for some particular events.

















