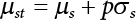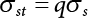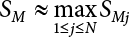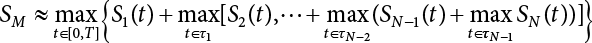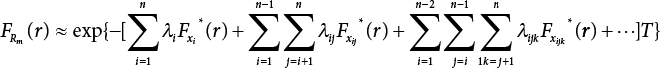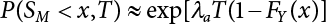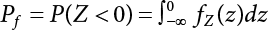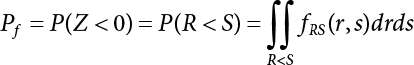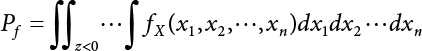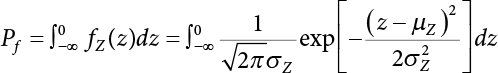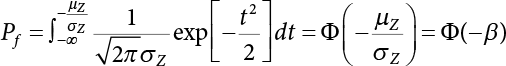Civil engineering is the general term for all sciences and technologies involved in the construction of various land engineering facilities. It is a technical discipline that studies engineering facility structures, as well as rock, soil and the environment, and their interaction with engineering facilities. Civil engineering is the cornerstone of national economic development, the bearing structure of all industrial and civil buildings, bridges and aqueducts built across rivers and lakes, breakwaters built in oceans, as well as sea-crossing bridges and offshore platforms. These constructions are primarily made of steel, wood, masonry, concrete and reinforced concrete, and are collectively referred to as engineering structures. They are designed to carry loads consisting of equipment, people and vehicles, and to withstand wind, rain, snow, sunshine, waves, currents, earth pressure and earthquakes. Whether the engineering structure is safe or not has a direct bearing on people’s property, lives, safety and health, as well as on the progress of national modernization. Therefore, an engineering structure should be able to perform a variety of designed functions during its service life, without the need for excessive maintenance, while ensuring the safety, serviceability and durability of the structure. These are the basic concepts of engineering structural reliability [1-1][1-2][1-3]. There are some uncertainties in terms of structural design and use, which will inevitably affect structural resistance and load effect to a certain extent. In the early stages of structural design, people sometimes evaluate the influence of uncertainty on an engineering structure by means of a safety factor. This is also used as an evaluation index for civil engineering, without taking the randomness of these uncertainties into account. In fact, the relationship between safety factor and structural reliability is not all that clear, since structures with the same safety factor may have different levels of reliability. This demonstrates that the safety factor alone cannot accurately reflect the reliability of engineering structures. Structural reliability is a subject concerning uncertainty research, and is designed to ascertain the effects of uncertainties arising from the entire life cycle of an engineering structure (including design, construction, application and maintenance) on its safety, serviceability and durability. With the development of computational science, engineering structures are required to be increasingly precise and intelligent, but in practice, the design and construction of engineering structures remains an iterative process in the conventional sense, far from being able to meet the needs of social development. If the uncertainty of design parameters is not taken into account, the benefits of accurate structural analysis will be overwhelmed by the use of safety indices determined roughly from experience. Therefore, it is of great significance to take parameter randomness into reasonable consideration during engineering design. Structural engineering should not only meet the pre-defined functional requirements, but also help to save costs as far as possible. This requires paying attention to the uncertainties existing in practical engineering, so that the structure can be designed scientifically using a more rational and realistic method, that is to say, a design method based on structural reliability [1-4][1-5][1-6][1-7][1-8][1-9][1-10][1-11][1-12][1-13]. Moreover, the reliability of in-service structures cannot be ignored either. This is because there are also many uncertainties arising from the construction and use of an engineering structure. These include load uncertainty, environmental uncertainty, resistance uncertainty, and effect uncertainty. Such uncertainties may bring about potential safety hazards, which may in turn lead to structural failure, resulting in a disastrous accident, causing great economic losses and endangering people’s lives and safety [1-14][1-15][1-16][1-17][1-18][1-19][1-20][1-21][1-22]. Therefore, it is imperative to analyze and evaluate the reliability of all engineering structures [1-23]. Compared with structural uncertainties, the uncertainties of loads and load effect on structures are even more important. Generally speaking, the environmental effects on engineering structures, such as wind load, temperature action, seismic action and marine environmental impact, are all reflected in a random fashion, while the environmental effects of structural design are expressed as extreme values, quite different from how the environment acts in nature. However, as far as structural design is concerned, it is necessary to take its reliability into consideration [1-24]. Therefore, the environmental effects on structures, and their dynamic impact, constitute the scope of dynamic structural reliability. This is extremely important for the reliability of an engineering structure throughout its life cycle, requiring the highest degree of attention [1-25]. In the early 1920s, Mayer et al. [1-26] applied the probability theory and mathematical statistics to the reliability analysis of engineering structures. In 1947, Freudenthal [1-27] published an article titled “The Safety of Structures”, marking the beginning of systematic research on how to apply reliability to structural design. In the 1950s, the concept of “reliability” had drawn widespread attention in the field of civil engineering. In the 1970s, researchers focused more on how to use the reliability method for structural design specifications. Later, some countries introduced reliability into their national standards, ushering in a period of practical application. Since the 1980s, research on the reliability of engineering structures has risen to the system level. Today, many countries now pay increasing attention to reliability research, with it having extensive applications. The research on structural reliability primarily focuses on the following aspects: (i) basic theory of structural reliability and associated calculation methods; (ii) issues related to the reliability of structural systems; (iii) issues related to the reliability of structures under dynamic loads; (iv) issues related to the reliability of a structure’s fatigue load; (v) issues related to the reliability of geotechnical engineering structures; and (vi) issues related to evaluation of the reliability of in-service engineering structures. Structural reliability, which is theoretically based on the probability theory, focuses on the determination of functions, the search for failure modes, the calculation of failure probability, and the characteristic statistics of random variables. Major calculation tools include the finite element method (FEM), the boundary element method (BEM) and network analysis techniques, while the main calculation methods include numerical simulation, proximate calculation, optimization and intelligent analysis. (1) Fast integration methods Fast integration methods include the first-order reliability method (FORM), the second-order reliability method (SORM) and other higher-order reliability methods, of which FORM and SORM are most commonly used for reliability analysis in engineering practice. In 1974, Hasofer and Lind [1-28] expanded the limit state equation at the checking point, and proposed an improved FORM, known as the checking point method. On this basis, Rackwitz and Fiessler [1-29] proposed a checking point method that could consider the actual distribution of random variables. Later, the Rackwitz-Fiessler method was adopted by the Joint Committee on Structural Safety (JCSS), and named the “JC” method. Marked by the put-forward of the “JC” method, FORM effectively reached maturity for use in reliability analysis in the 1980s, and there was little foreign research literature on FORM published after the 1990s. In 1996, Zhao Guofan et al. [1-30] associated relevant random variables with generalized stochastic space on the basis of their practical analysis method, further proposing a method for processing non-normal variables and associated random variables. The calculation of the partial derivative of variables in the limit state equation is an important part of reliability calculation by FORM. Xu Jun et al. [1-31] proposed a partial derivative calculation method for rational polynomial functions with regard to highly nonlinear and complex limit state equations. The Rosenblatt transformation is decomposed in reference [1-32], with the relevant normally distributed variables transformed into irrelevant normally distributed variables through mapping transformation, and then into independent standard-normally distributed variables through orthogonal transformation, deriving a more general and applicable form of FORM. For structural reliability analysis, Fiessler et al. [1-29] first proposed an SORM considering the second-order surface effect that could be used for second-order expansion at the design point in U space. Then, Breitung [1-33] proposed an asymptotic formula considering the effects of the principal curvature of the limit state surface at the checking point for failure probability calculation using SORM. This formula is now widely applied in reliability analysis. Although SORM already effectively achieved maturity in the 1990s thanks to the efforts of academic researchers at home and abroad, especially Fiessler, Rackwitz, Tvedt and Breitung [1-29][1-34][1-35], even more progress was made in SORM research in later years. Considering the difficulty in calculating the Hessian matrix in SORM, Der Kiureghian [1-36], Zhao Yan-Guang and Tetsuro Ono [1-37][1-38] adopted empirical points for fitting the curves, obtaining a quadric curve and revealing the principal curvature of the surface, thus further improving SORM. Li Yungui [1-39] applied Laplace’s integral approximation theory to the approximate calculation of reliability in generalized stochastic space and orthogonal random space. This method is applicable to the high nonlinearity of functions; the asymptotic method remains the type of SORM that also considers the use of the second partial derivative term in a nonlinear function; when used to calculate the reliability index, this method shows good accuracy by taking the partial derivative of the limit state equation and obtaining Taylor’s series, but it is troublesome to solve some complex functions that are difficult to take the derivative of. In 1998, Der Kiureghian and Dakessian [1-40] proposed a reliability calculation method for multi-design-point limit state equations. Calculation accuracy and calculation complexity are often contradictory to each other, making it necessary to choose calculation methods with varying levels of complexity for different objects. In 1999, Zhao Yan-gang and Tetsuro Ono [1-41] set conditions suitable for both FORM and SORM. Some researchers have explored higher-order reliability calculation methods. Tichy [1-42] proposed a first-order third-moment reliability calculation method; Zhao [1-43][1-44] proposed a higher-order moment reliability analysis method by normal transformation of variable order moments; Zhao et al. [1-45] proposed a fourth-moment analysis method for reliability calculations. In conclusion, although SORM is already well established, academic researchers at home and abroad have improved it in different aspects, enhancing its serviceability. Considering its low calculation complexity, SORM shows good accuracy when used to solve linear and weakly nonlinear limit state equations. However, because higher-order methods have a more complex calculation process than SORM, and since the larger the number of expansion times, the higher the order and the higher the calculation complexity, there is no generally recognized short-cut calculation method with strong serviceability. What is worse, there is no significant improvement in accuracy, meaning such methods are rarely adopted for reliability analysis in engineering practice. (2) Numerical simulation methods The fast integration methods for reliability calculation, such as FORM/SORM, are quite similar to each other in how they handle the nonlinear and non-normally distributed variables of nonlinear limit state equations. Errors become obvious if the limit state equations are highly nonlinear. The Monte-Carlo method has been brought to the forefront so that it can be used to obtain more accurate results for structural reliability calculations. The Monte-Carlo method is a numerical simulation method based on the probability and statistics theory. This method avoids some of the mathematical difficulties that arise from the process of structural reliability analysis, making it unnecessary to consider the nonlinearity of functions or the complexity of the limit state surface. It is highly intuitive, accurate and applicable. However, the frequency of simulation in the Monte-Carlo method is inversely proportional to the failure probability, while the failure probability of structures is usually very low. So, when the Monte-Carlo method is directly adopted for reliability analysis, the sampling size must be very large in order to ensure satisfactory accuracy. But owing to its poor efficiency, the Monte-Carlo method is difficult to apply to the reliability analysis of actual engineering structures. For this reason, it is very important to find a way of improving the efficiency of the Monte-Carlo method. At present, variance reduction techniques are used to improve simulation accuracy, including antithetic sampling, conditional expectation variance reduction, importance sampling, stratified sampling, controlled variables and correlated sampling. Importance sampling is one of the most widely used, effective and popular variance reduction techniques for the calculation of structural reliability. Commonly used importance sampling methods include general importance sampling, updated importance sampling, adaptive importance sampling and directional importance sampling [1-46]. The computing paradigm in the importance sampling method, proposed by Melchers [1-47] is quite representative and often adopted by other researchers. In this method, the probability density function of an N-dimensional independent normal distribution is taken as the sampling function, while the design point obtained by SORM is taken as the center point, achieving good results. Hohenbichler and Rackwitz [1-48] proposed an updated importance sampling method, one based on the reliability index obtained by FORM or SORM. The distance from the sampling point along β to the failure surface in normal space is calculated to iteratively correct and update the calculation results of failure probability. This method is suitable for the actual form of the failure surface and has better adaptability to nonlinear problems. Also, calculation accuracy is improved due to the introduction of analytical methods. However, this method needs to constantly solve the limit state equations, leading to high calculation complexity when the limit state equations are hard to solve. Bucher [1-49] proposed an adaptive iterative search strategy to select a sampling center and sampling variance for importance sampling, and built an adaptive importance sampling method. It requires a little preliminary analysis, but the initial checking point and sampling variance, which are difficult to determine, have great influence on the convergence of the calculation. In 1999, Au and Beck [1-50] created an importance sampling point with the aid of Markov chains, and proposed a new adaptive sampling computation framework. With good robustness, this method is unaffected by the level of failure probability and the shape of the limit state surface. Directional sampling is a method by which samples are taken randomly along the direction of a radius vector in the spherical coordinate system to analyze structural reliability. The directional importance sampling method was first proposed by Au and Beck [1-51]. Later, Ditlevsen, Melchers and Gluver [1-52] applied this method to reliability analysis. The basic idea of directional importance sampling is as follows. Considering that the distance from each sampling point to the origin of coordinates in the N-dimensional independent standard normal space obeys the N-DoF distribution, truncated probability density without the β spherical domain can be taken as an importance sampling function to calculate the failure probability. Jin Wei-Liang [1-53][1-54] combined the importance sampling technique with conditional expectation variance reduction, putting forward a composite importance sampling method. Owing to the adoption of conditional expectation variance reduction, the sampling points are limited in the failure domain, thus raising the effectiveness of sampling, while the importance sampling function of truncated distribution helps to improve the efficiency of the sampling calculation. Through an orthogonal transformation, the original random variables are switched into another standard random space, with a V-space importance sampling method established that fully considers the geometric characteristics of the failure surface (e.g., maximum likelihood, gradient, curvature, etc.). Dong Cong et al. [1-55] solved the problem of seeking all design points in the generalized multi-design point problem based on a generalized genetic algorithm that he had proposed for global optimization of nonlinear systems in an unconnected domain. By establishing a recursive bound-tolerance algorithm, they solved the problem of compression and combination for generalized multi-design points, and advanced a theory of adaptive importance sampling based on the generalized genetic algorithm. Wu Bin, Ou Jinping et al. [1-56] analyzed the characteristics of structural dynamical reliability, proposed an importance sampling method, and put forward a method for selecting importance sampling functions and a concrete expression for them with respect to white noise load. When the Monte-Carlo method is used to analyze problems, a random number should be generated first; samples then need to be taken randomly according to the probability distribution of random variables. Although the frequency of sampling can be brought under control thanks to improvements in sampling technology, for a large and complex structure, the calculation complexity remains very high, making its use somewhat limited. The sample size should be minimized in order to improve calculation efficiency. At present, a number theory-based method, such as computer sampling or Latin sampling, is often used to generate a pseudo-random number in place of randomly collected samples for reliability analysis. The Latin hypercube sampling method is used directly for failure estimation, but its efficiency is poor. It has little obvious advantage compared with direct Monte-Carlo simulation. Olsson, Sandberg and Dahlblom [1-57] combined Latin hypercube sampling with importance sampling, putting forward an importance sampling method based on Latin sampling, and then proposed a measure for reducing the correlation among Latin sample points and a solution for orthogonal space. Examples show that this method can effectively improve the efficiency of numerical simulation. Wu and Zhao [1-58] proposed a number theory-based method for solving multi-dimensional normal distribution functions. This method can be used to precisely calculate the failure probability of a structural system; examples show that this method has enough accuracy. In summary, numerical simulation is easy to perform and capable of solving problems efficiently, but the effectiveness of direct analog computation is very low, making it imperative to develop a high-efficiency numerical simulation method. Researchers throughout the world have done a lot of work to improve the performance of numerical simulation, with a variety of new high-efficiency algorithms being proposed. As can be expected, new high-performance numerical simulation methods will surely emerge in large numbers with the development of computer software and hardware technology. (3) Responding surface method During the reliability analysis of complex structures, structural functions cannot normally be (or are not) expressed explicitly; furthermore, only some discrete empirical points can be obtained by numerical algorithms (e.g., FEM) or from experimental studies. If Monte-Carlo simulation is used for reliability analysis, extensive numerical analysis will have to be conducted. Under the circumstances, the responding surface method is therefore a good choice. Wong [1-59] first proposed a quadratic polynomial responding surface method for reliability calculations, using quadratic polynomials containing linear terms and cross terms to approximately fit the real limit state of structures, and then locating the sampling center at the average point. When there are many random variables, the number of samples required for fitting will increase rapidly when adopting this method. Moreover, it will be difficult to reflect the main characteristics of the failure surface if the sampling center is located at the average point. Later, Bucher et al. [1-60] improved this method, with the cross terms in the quadratic polynomials ignored and the quadratic terms retained. At the same time, the sampling center was approximately located on the failure surface due to a linear interpolation between the average point and the checking point obtained by fitting. When Bucher’s method is adopted for calculation, only 2n+1 experimental point is needed to uniquely determine 2n+1 unknown number. However, when Bucher’s iterative strategy is used for calculation, the convergence process may be unstable owing to obvious fluctuations in the response surface during iteration. This is because the sampling center is likely to come from extrapolation. Therefore, Rajashekhar [1-61] gave different weights according to the distance between the empirical point and the real limit state surface in a bid to maximize the fitting precision of the limit state equations at the design points, thereby improving the accuracy of failure probability calculations. Kim [1-62] projected the sampling point onto the linear response surface so that it could be as close to the response surface as possible, enhancing the convergence of the method. In recent years, Lee [1-63], Wong [1-64] and Kaymaz [1-65] have also been committed to improving the nonlinear fitting ability of the responding surface method, reducing its calculation complexity and increasing its accuracy. By learning the samples obtained from finite element calculation, neural networks can precisely fit those highly nonlinear functional relations which are difficult to accurately express by means of general analytic expressions [1-66][1-67][1-68][1-69]. Tong and Zhao [1-70] combined the quadratic polynomial responding surface method with the geometric method for reliability index selection, accelerating the convergence speed of iteration. Gui and Kang [1-71] applied intelligent computing techniques, such as neural networks, fuzzy mathematics and genetic algorithms, to the reliability analysis to systematically study the intelligent calculation methods essential for neural network response surface reconstruction, achieving a good effect. The Support Vector Machine (SVM) is a new AI technique that has many advantages [1-72] over quadratic polynomials and neural network function fitting. Yuan [1-73] carried out research into the application of a least squares support vector machine (LS-SVM) to reliability calculations, achieving good results. In short, the responding surface method is an ideal method for analyzing the reliability of large and complex structures in implicit limit state equations. Traditional quadratic polynomial methods have limited nonlinear fitting ability, meaning AI techniques, such as neural networks and genetic algorithms, as well as fuzzy mathematics, can be applied to reliability analysis. SVM is a new AI technique with excellent small sample processing ability which has been developing rapidly in recent years. The responding surface method has small samples, meaning the SVM-based responding surface method has broad research and application prospects. The reliability analysis of actual engineering structures is usually not just a matter of calculating the reliability of a failure mode, a component or a surface, but involves calculating the reliability of structural systems in multiple functions. The probability of system reliability was worked out during the early stages of reliability development. In 1969, Cornell [1-74] proposed a wide-bound formula for the interval estimation method applied to system reliability calculation. In 1979, Ditlevsen [1-75] found that for some examples, an excessively large range of system failure probability was obtained by Cornell and Moses’ method [1-76], and therefore proposed a narrow-bound formula for system reliability calculations. Ang et al. [1-77] applied the idea of fault tree analysis to the reliability of structural systems, and proposed a point estimation method, i.e., the probabilistic network evaluation technique (PNET) for system reliability analysis. With the establishment of the above theory, an available solution can be developed for system reliability analysis under the condition that the main failure modes are known. But due to the difficulties in mathematical and mechanical analysis, the research on system reliability has developed very slowly. So far, the related achievements have not yet been put into practice. Numerical simulation is also a good method for calculating the reliability of structural systems. Nie and Ellingwood [1-78] simulated the reliability of structural systems using Fekete points generated in advance; their findings show that compared with other homogeneous point generation techniques (t-design, GLP), Fekete points are more homogeneous and require fewer sampling points to replace random dots for the analog computation of reliability. In this way, the frequency of finite element analysis (FEA) can be effectively reduced when a finite element program is used for structural calculation. But like other pseudo-Monte-Carlo methods, this method has insufficient accuracy when variable dimensions are high. In the late 1960s, Hasofer [1-79] proposed a combination of persistent floor live load with temporary floor live load. Although this combination rule was not applied to engineering practice, the idea of this combination will continue to guide and promote the development of the “Loads and Load Combination Method”. Der Kiureghian [1-80] introduced FORM into the load combination method, proposing a first-order second moment rule for load combinations. It is argued that the first and second moments μst and σst of the maximum value distribution of a single load effect in the design reference period [0, T] can be expressed by the first second moments μs and σs distributed at any time point. The change of parameters p and q in the above equations, as well as their value, is related to the type of load process and the average frequency of load occurrence in [0, T]. It is very inconvenient to use the parameters p and q in engineering practice, but this load combination rule, which boasts a unique idea and a simple method, helps to promote the innovation of theoretical research on random load combination. In 1970, Turkstra [1-81] and Larrabee [1-82] proposed a load combination rule (referred to as the TR rule) from a practical perspective. It is argued that in a load combination, a certain load reaches its maximum in the reference period, while the remaining loads occur at any given time point. Therefore, when N variable loads are combined, they play a dominant role in turn. The maximum value in [0, T] can be combined with the value of the remaining N-1 loads at any time point to form N combinations. The controlling value is taken as the approximate value of the maximum load, as follows where SMj represents the maximum value of the j-th load in [0, T], i.e., In 1972, Ferry-Borges and Castanheta [1-83] proposed the isochronous load combination model based on Turkstra’s idea. This then became the basis for giving advice on load combinations in the Canadian Construction Specifications. The expression of this model is shown in Equation (1.4). where S1(t), S2(t), …, SN(t) are the loads to be combined, while SM represents the maximum value of the load combination. In 1976, JCSS proposed another load combination rule (the JCSS Combination Rule). It is assumed that the stationary binomial process is uniformly selected as a probability model for the random load process {Si(t), t ∈ [0, T]}, (i = 1, 2, ⋯, N). The total number of time intervals for every Si(t) in [0, T] is flagged as ri, which is arranged in order of magnitude of ri(r1 ≤ r2 ≤ ⋯ < rN). In the combination process, the maximum value of a certain load, Si(t), in [0, T] is taken in turn. Regarding the loads for which there are more than ri time intervals in [0, T], the local maximum value at the previous time interval is taken, while the relevant instantaneous value is taken for the remaining loads. In this way, N combinations can be formed, with N relatively maximum loads obtained. After this, a group of results that play a controlling role can be taken as an approximation of SM. Wen [1-11] came up with an idea similar to Hasofer’s rule, and further studied how to combine class-a loads with class-b loads, with the load combinations divided into two types: where λi is the average occurrence rate of i-th action. λij = λiλj (μdi + μdj), λijk = λiλjλk (μdi μdj + μdj μdk + μdk μdi), where Larrabee [1-82] studied the problem of load combinations involved in various loading processes. The load combination rule proposed by Wen [1-84] is also of great theoretical importance and rigorously reasoned, and boasts highly accurate results, but there only a few types of load models were adopted. However, many parameters are involved in the calculation, making it inconvenient to apply this rule in engineering practice. Usually, it is used to verify the accuracy of other load combination methods. Soares [1-85] discussed the combination of main load effects in ship structures. Floris [1-86] used the stochastic analysis method to study load combinations, and proposed a new practical analysis method. Casciati and Colombi [1-87] discussed load combinations and the related problem of fatigue reliability. Naess and Royset [1-88] generalized Turkstra’s rule and applied it to related load effect combinations. Gray and Melchers [1-89] studied the problem of load combination by means of load space simulation, and Ellingwood [1-90] studied the problem with respect to structures. Wang and Padgett [1-91] corrected the load coefficient for reinforced concrete bridges under the combined action of earthquakes and erosion. Meimand and Schafer [1-92] investigated the effect of load combinations on the reliability of cold-formed flexural steel members. Al-Sibahy and Edwards [1-93] proposed a method for testing the performance of new concrete block walls under the combined action of axial loads and thermal exposure. Hmidan [1-94] investigated the combined effect of sustained load and low temperature on the flexural performance of damaged steel beams repaired with CFRP. Lantsoght [1-95] built an extended strip model for slabs considering the combined action of loads. Xu [1-96] built a method for simplifying the aseismic design of high-rise buildings in a vertical composite framework system. Feng and Dai [1-97] studied the modes of load combinations on high-speed railway bridges, and calculated the partial load factor in accordance with the statistical parameters of high-speed railway bridge loads and resistance by reference to the target reliability index presented in the Code for Design on the Steel Structure of a Railway Bridge. Chen [1-98] explored load combinations in structural design. By introducing the isochronous load models widely used in other applications together with the relevant combination theories, he proposed theoretical formulas for the partial load factor and combination coefficient, and explained how to apply these formulas and theories within the load code. He also pointed out that, since load combinations are under the control of the permanent load, structural reliability can be adjusted automatically under a design condition dominated by structural weight. This would occur based on the load combination rule in the revised load code, without the need to deliberately improve the safety factor for different specific occasions. Dai [1-99] introduced and analyzed the possible common effect of load combination value changes on structural design according to the revised code for the design of building structures. They then gave examples based on probability theory for comparison, and pointed out problems that should be brought to the forefront and further explored. Ou Jinping et al. [1-100] determined the probability distribution of amplitude and random variables in any period of the random load combination process in accordance with the principle of maximum entropy. Then, by reference to the code design method, they discussed the assurance rate of the load combination coefficient, and conducted the Monte-Carlo test, verifying the accuracy of this load combination method. Gong and Zhao [1-101] proposed an analytic solution and a simplified calculation formula for the probability distribution function with respect to the combination of persistent variable load and temporary variable load. Su [1-102] introduced the provisions on loads and load combination in the second part of the British code BS5400, providing load data for load conversion in a bridge design made under BS code using homemade software. He pointed out that, from the perspective of the total load effect, the BS code focuses on safety while the Chinese code focuses on cost-effectiveness. Gu Ming et al. [1-103] established a joint probability distribution function for the effect of wind loads on high-rise buildings in two orthogonal directions based on high-frequency force balance experiments and the Copula Frank function. The wind load combination coefficient was calculated at a specific assurance rate. Li [1-104] considered the correlation between wind-wave elements, adopting Gumbel’s joint probability model to successfully combine water flow with wind by means of wind currents. To study the effects of wind load, wave load and environmental load, along with their combinations on sea-crossing bridges, they combined wind load with wave load by means of the combination model proposed by JCSS. To sum up, Chinese and foreign researchers have focused on different things while studying and applying random load combinations, which remains a core part of reliability theory [1-104]. Foreign researchers have concentrated on in-depth studies of the theory of random load combinations based on the engineering reliability theory, and have proposed different load combination rules. Chinese researchers have focused on the application of the existing random load theory, and applied this to random load combinations in the construction of roads and bridges, high-speed railways, and civil buildings. Thanks to its continuous development and improvement, the reliability theory has laid a solid foundation for the safety evaluation of engineering structures such as industrial and civil buildings, bridges and marine structures. At present, the priority for the practical application of reliability theory has been shifted from the reliability of a single structural component (including time-independent reliability and static reliability) to the reliability of a complex system. This includes time-dependent reliability, life-cycle reliability and dynamic reliability. Many outstanding academic researchers throughout the world have carried out research into this form of reliability, achieving a series of excellent results. Representative foreign researchers include Frangopol, Moan and Ellingwood. Based on the basic principle of reliability, Frangopol et al. [1-105][1-106][1-107][1-108][1-109][1-110][1-111] conducted an in-depth study on the life-cycle reliability of concrete structures and marine structures from the perspective of materials, corrosion, fatigue and repair. Moan et al. [1-112][1-113] [1-114][1-115][1-116][1-117][1-118][1-119][1-120][1-121][1-122][1-123] conducted extensive research on the reliability analysis of typical offshore structures such as fixed platforms, floating platforms, offshore wind turbines and submarine pipelines, and calibrated the reliability level of various offshore structures, greatly promoting the application of reliability theory to offshore engineering. Ellingwood [1-61] [1-124][1-125][1-126][1-127][1-128] has also made outstanding contributions to the development of reliability-based structural design theory, as well as structural safety evaluation and risk analysis. Chinese academic researchers started studying reliability in the 1950s. In the 1960s, Zhao Guofan published a monograph titled “Engineering Structural Reliability” [1-30], and published Structural Reliability Theory [1-31] in the early 21st century, reflecting China’s latest achievements in reliability research. Gong Jinxin [1-4][1-30][1-31][1-32][1-129][1-130][1-131] continues to carry out research into the reliability analysis method in generalized random space considering inter-variable correlation, as well as high-precision SORM, the fourth moment method, the system reliability method and the time-dependent reliability method for concrete structures. Wang Guangyuan and Lü Dagang et al. [1-6][1-132][1-133][1-134][1-135][1-136][1-137] have done a lot of research on the seismic reliability of structures. Li Jie and Chen Jianbing et al. [1-25][1-138][1-139][1-140][1-141][1-142][1-143][1-144][1-145][1-146] conducted an in-depth study on stochastic dynamics and the seismic reliability of large-scale complex engineering networks, advancing a network connection reliability analysis theory centered on the recursive decomposition of structural functions. This enabled them to create a moment method system for the functional reliability analysis of large-scale complex engineering networks. Xu Jun et al. [1-147][1-148][1-149][1-150][1-151] conducted an in-depth study on the efficient numerical methods of structural dynamic reliability by combining stochastic structural dynamics with the random finite element analysis of structures. Jin Wei-Liang et al. [1-152][1-153][1-154][1-155][1-156][1-157][1-158][1-159][1-160] [1-161][1-162][1-163][1-164][1-165][1-166][1-167][1-168][1-169][1-170][1-171][1-172][1-173][1-174][1-175][1-176][1-177] [1-178][1-179][1-180][1-181][1-182][1-183] have done extensive research on the strength and fatigue reliability of fixed offshore platforms, as well as on the overall strength and fatigue reliability of floating platforms, the fatigue reliability of submarine pipelines and the vibration comfort of engineering structures. Reliability theory is now being applied to numerous engineering structures in various fields. With the continuous development of computer technology and the accumulation of actual engineering data, it is virtually guaranteed that the theory will continue to be built upon. Reliability theory thus plays an increasingly vital role in engineering design, evaluation and operation. This section presents a basic description of the main concepts related to the reliability theory, methodology and application. During the life cycle of an engineering structure, it must be able to function normally. The life cycle is a whole process, composed of structural design, construction, operation, maintenance, repair, reinforcement, transformation, demolition and reuse. There should be special requirements for structural performance in these different periods. Structural reliability refers to the ability of a structure to fulfill its preset functions (safety, serviceability and durability) within the prescribed time under the specified conditions. The above-mentioned prescribed time is defined as the working life of a structure as given in the Unified Standards for the Reliability Design of Engineering Structures, while the specified conditions mean that the structure should meet the requirements for normal design, construction, use and maintenance. The preset functions refer to structural safety, serviceability and durability. The requirements for these functions are as follows: (1) be able to bear various types of pressure arising from construction and use; (2) maintain good functional performance; (3) have enough durability; (4) be able to maintain enough bearing capacity in case of fire; and (5) be able to stay stable in case of an accident, such as explosion, impact or artificial destruction. Therefore, structural reliability is the generic term for structural safety, serviceability and durability. Structural reliability refers to the ability of a structure to fulfill its preset functions within the prescribed time under the specified conditions. Structural reliability is also the probabilistic measurement of the reliability of a structure. Failure probability refers to the probability that the preset functions fail to be exerted. The structural reliability must be set with the cause and mode of structural failure in mind (e.g., for a structure or structural component that collapses suddenly without warning, its reliability should be higher than that of a structure or structural component which can collapse before failing). It must also consider the possible consequences of failure, such as the human, material and financial resources needed to reduce the risk of failure, as well as specific social and environmental conditions. Structural reliability is used to mathematically measure the effects of structural uncertainty on structural safety, serviceability and durability throughout a structure’s life cycle. Structural uncertainty refers to the inability to accurately foresee what is going to occur to a structure or structural component, and means that there is no inevitable relationship between the conditions required for a possible occurrence and its consequences. Structural uncertainty, which exists throughout the life cycle of a structure, manifests itself in the inability to precisely know the active state of the structure, particularly the distribution of consequences and losses. Structural uncertainty can be classified based on a structure’s characteristics, manifestations, internal relations and attributes, such as randomness, fuzziness and knowledge imperfection. It falls broadly within the domain of objective and subjective uncertainties, physical, statistical and model uncertainties, and parameter and system uncertainties. Structural uncertainty analysis methods can be classified into probability-based reliability calculations, fuzzy concept-based reliability calculations, gray theory-based reliability calculations and entropy theory-based reliability calculations, depending on the uncertainty classification. Structural reliability and unreliability are uncertain events, brought about by the uncertainty of relevant variables. In structural reliability analysis, these variables are usually regarded as time-independent random quantities, and include random variables random functions, and time-dependent random processes. Structural design and analysis are processes in which qualitative analysis is combined with quantitative calculation. Quantitative calculation refers to the mathematical and mechanical methods used to calculate the variables involved. In reliability theory, the variables directly used for design calculation are called basic random variables, such as load, material strength, modulus of elasticity, and component size. The probability characteristics of random variables can be described in terms of their probability density function and probability distribution function. The statistical features of random variables are often used to reflect a certain probability characteristic of theirs. For example, the average value (first moment) reflects the degree of concentration of random variables, while the variance (second moment) reflects the degree of dispersion of random variables. For a two- or higher-dimensional random variable cluster, it can be expressed by the random variable function X (x1, x2, …, xn) and by the random function X. The stochastic process X(t) is a random function based on time t, where the value of X is a random variable at any time point. The value of X(t) is determined by its probability density function fX(x, t). Of course, the variable t can be replaced by any set of finite, or countable, infinite values, such as the number of loads applied. Therefore, the stochastic process X(t) can be divided into a continuous stochastic process and a discrete stochastic process. When the entire structure or a part of the structure exceeds a specific state, a certain preset function will fail to be exerted. This specific state is known as the limit state of the function. Therefore, when a structure or component is in its limit state, a relational expression of various relevant basic variables will be formed. This is called the limit state equation. The working state of the structural component within which it exerts its preset functions can be described with the relationship between action effect S (referring to the internal force and deformation caused by load, such as axial force, bending moment, shear force, deflection or crack width of the component) and structural resistance R (referring to the ability of the component to resist the action effect, such as the cross-sectional strength and stiffness of the component). This expression is known as the structural function, and is represented by Z=g(R, S). The probability of having the preset functions exerted within the prescribed time under the specified conditions is known as reliability probability, while the probability of failing to have the preset functions exerted under the above conditions is called failure probability. In engineering practice, structural failure is the focus of concern, and failure probability is mostly used to reflect structural reliability. When the function Z = R − S, the probability of structural failure is calculated according to the following formula: Equations (1.7) and (1.8) offer formulas for failure probability given known probability distributions of the structural function. Generally, the distribution of Z depends on the probability distribution of the random variables contained within it, and on the form of the function. When the function contains n random variables, structural failure probability is expressed as: As can be seen, the classical integral expression is a high-dimensional integral, and its dimensions are the same as the number of random variables. When there are many random variables, it is very difficult to perform calculations directly and apply it to engineering practice, which is why the reliability index needs to be introduced. It is assumed that Z obeys normal distribution and that its average value is μZ while its standard deviation is σZ. Therefore, structural failure probability can be given as follows where The reliability probability of a single component is called component reliability; the reliability probability of an overall structure is called system reliability. An actual engineering structure is complex, and ultimate structural failure depends on the overall behavior of a structure. The research on the failure of the overall structural system is an important aspect in reliability. Because the failure of the entire structure is caused by the failure of a structural component, the failure probability of the entire structure can be estimated according to the failure probability of each structural component. If the structural state remains unchanged throughout the service period, reliability is referred to as time-independent reliability. In engineering practice, some variables are random and time-dependent. For example, the variable load acting on a structure changes from time to time, and this structure will not be considered safe unless it is in a secured state at every moment of its service life. Thus arises the problem of time-dependent reliability. The problem of time-dependent reliability can be first converted into a problem of time-independent reliability by mathematical methods before being solved. Therefore, the solution to the problem of time-independent reliability is the basis for all reliability theory. This book first introduces the related concepts and calculation methods for structural reliability, and then analyzes the reliability of actual engineering structures. The content is divided into the following parts: This book introduces the basic theory and analysis methods of structural reliability. The contents are as follows: An overview of the basic theories and concepts of reliability, uncertainty analysis, reliability calculations, numerical simulation of reliability, system reliability analysis, reliability of time-varying structures, loads and load combinations, and standard application of reliability. Characterized by a combination of theory and practical engineering, this book systematically describes the latest research achievements in reliability theory to promote the development of reliability theory in engineering practice. In this way, it provides a reference for improving and revising the unified standard of structural reliability. The book is characterized by a combination of theory and actual engineering, meaning it can be used as a textbook and teaching reference book for graduate students and senior undergraduates majoring in civil engineering, water conservancy, highway engineering, railway engineering, port engineering, shipbuilding and maritime engineering. It is also a professional reference book for engineers, technicians and academic researchers engaged in the research and design of civil and industrial architecture, municipal facilities, bridges, roads (highways and railways), ports and marine facilities.
1
Introduction
1.1 An Overview of the Development of Structural Reliability Theory
1.1.1 Method of the Degree of Reliability Calculated
1.1.2 Reliability Method of Structural Systems
1.1.3 Load and Load Combination Method
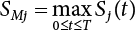 , which is the relative maximum value among the values of the remaining N-1 loads at any time point.
, which is the relative maximum value among the values of the remaining N-1 loads at any time point.
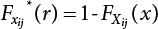 , where
, where 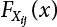 represents the overlap between two loads, Si(t) and Sj(t).
represents the overlap between two loads, Si(t) and Sj(t). 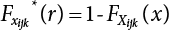 , where
, where 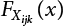 represents the overlap among three loads, Si(t), Sj(t) and Sk(t)
represents the overlap among three loads, Si(t), Sj(t) and Sk(t)
 .
.
1.1.4 Engineering Applications
1.2 Basic Concepts
1.2.1 Reliability and Degree of Reliability
1.2.2 Uncertainty
1.2.3 Random Variables, Random Functions and Random Processes
1.2.4 Functional Function and Limit State Equation
1.2.5 Reliability Index and Failure Probability
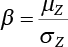 it called the reliability index, which has a one-to-one correspondence with failure probability.
it called the reliability index, which has a one-to-one correspondence with failure probability.
1.2.6 Member Reliability and System Reliability
1.2.7 Time-Dependent Reliability and Time-Independent Reliability
1.3 Contents of this Book
References